Lateral stability is a critical aspect of structural design, especially in regions prone to strong winds and seismic activities. In Australia, structural engineers familiar with calculating wind loads and earthquake or seismic loads according to the AS/NZS 1170:2021 series must design lateral stability systems (also known as lateral force resisting systems) to ensure the stability of the structure in resisting these loads in residential and commercial buildings.
This article focuses on various structural elements and systems used for lateral stability, exploring their benefits, disadvantages, design procedures, and considerations. All design examples follow the procedures specified in Australian Standards.
Braced Frames
Braced frames are a common lateral stability system, providing strength and stiffness against lateral loads. They consist of diagonal bracing members that resist lateral forces through axial tension or compression.

Figure 1: An example of braced framing system in a multi-level carpark
Use Case
Braced frames are suitable for a variety of building types and heights. They are particularly effective in low to medium-rise structures where architectural flexibility is not heavily compromised. Common use cases include:
- Warehouses: Braced frames offer efficient lateral stability for large open spaces typical of warehouses.
- Industrial Buildings: In industrial structures, braced frames provide stability without obstructing large working areas.
- Residential Buildings: Braced frames can be employed in mid-rise residential buildings, ensuring stability while allowing for flexible floor layouts.
Benefits
- Efficient in resisting lateral loads.
- Simple design and construction.
- Suitable for a wide range of building heights.
Disadvantages
- Limited architectural flexibility due to brace placement.
- Potential for interference with interior spaces.
Design Procedure
- Step 1: Identify bracing locations based on structural analysis.
- Step 2: Select appropriate bracing members and connections.
- Step 3: Ensure compliance with AS 4100 for steel structures or AS 3600 for concrete structures.
Example
Given building dimensions and expected lateral loads, determine the required bracing locations. Calculate brace forces and member sizes based on AS 4100 or AS 3600.
- Building Height: 20 meters
- Lateral Load: 100 kN
- Bracing System: Diagonal braces in steel
- Material: Steel with yield strength, F y = 250 M P a F_y = 250MPa Fy?=250MPa
Design Procedure
Step 1: Determine Bracing Locations 1. Perform structural analysis to identify critical locations for bracing. 2. Assume bracing at corners and midpoints of each wall.
Step 2: Select Bracing Members 1. Calculate brace forces using the tributary area method. 2. Assume a tributary width of 5 meters for each brace. 3. F b r a c e = T o t a l L o a d N u m b e r o f B r a c e s = 100 k N 8 = 12.5 k N F_{brace}=\frac{Total Load}{Number of Braces}=\frac{100kN}{8}=12.5kN Fbrace?=NumberofBracesTotalLoad?=8100kN?=12.5kN
Step 3: Determine Member Sizes 1. Use AS 4100 for steel structures. 2. Select a suitable section (e.g., SHS 100x100x5) based on axial capacity. 3. Perform the calculation checks a. Determine brace forces F b r a c e = 12.5 k N F_{brace}=12.5kN Fbrace?=12.5kN b. Check axial capacity of selected section A g = 2 ? ( 100 ? 5 ) ? 5 = 950 m m 2 A_g=2*(100-5)*5=950mm^2 Ag?=2?(100?5)?5=950mm2 P n = 0.9 ? F y ? A g = 0.9 ? 250 M P a ? 950 m m 2 = 213.75 k N P_n=0.9*F_y*A_g=0.9*250MPa*950mm^2=213.75kN Pn?=0.9?Fy??Ag?=0.9?250MPa?950mm2=213.75kN F b r a c e < P n ? Therefore the design is safe. F_{brace} \lt P_n \longrightarrow \text{Therefore the design is safe.} Fbrace?<Pn??Therefore the design is safe.
Step 4: Verify the member selected using ClearCalcs� Steel Beam Design to AS 4100
Shear Walls
Shear walls are vertical elements designed to resist lateral forces, providing both strength and stiffness to the structural system.
They are often constructed using reinforced concrete in commercial buildings and timber in residential buildings, depending on the amount of lateral load. An example for the timber shear wall will be addressed later in the article under the combined systems heading.
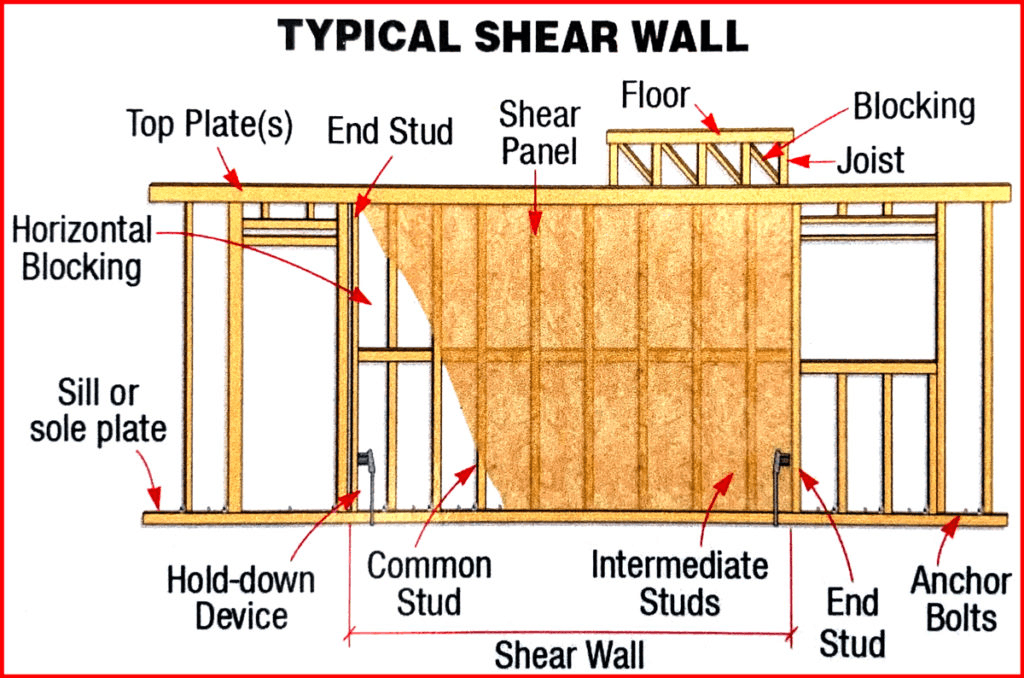
Figure 2: Timber shear wall

Figure 3: Reinforced concrete shear wall
Use Case
Shear walls are often chosen for their ability to efficiently resist lateral loads in high-rise buildings. They find application in structures where architectural flexibility and optimal space utilization are crucial. Key use cases include:
- High-Rise Residential Towers: Shear walls are commonly used in high-rise residential buildings to provide stability and maintain a slim structural footprint.
- Commercial Towers: In office buildings and commercial complexes, shear walls help resist lateral forces while accommodating various office layouts.
- Mixed-Use Developments: Shear walls are suitable for mixed-use buildings that combine residential, commercial, and retail spaces.
Benefits
- Efficient in resisting lateral loads, especially in high-rise buildings.
- Allows for architectural flexibility as they can be integrated into the building envelope, such as located in lift walls or stairwells.
Disadvantages
- May require careful detailing to prevent undesirable cracking.
- Challenging in retrofitting existing buildings.
Design Procedure
- Step 1: Analyze building layout to identify shear wall locations.
- Step 2: Select appropriate materials and reinforcement based on AS 3600 or AS 4100.
- Step 3: Ensure compliance with detailing requirements to prevent shear failure.
Commercial Building Reinforced Concrete Shear Wall Example
Determine the shear wall locations based on structural analysis and calculate required thickness and reinforcement based on AS 3600 or AS 4100.
Given Parameters:
- Building Height: 15 meters
- Lateral Load: 80 kN
- Shear Wall System: Reinforced Concrete Shear Walls
- Material: Concrete with characteristic strength
Design Procedure:
Step 1: Identify Shear Wall Locations 1. Perform structural analysis to determine optimal locations. 2. Assume shear walls at building ends or at internal lift shafts or stairs
Step 2: Select Shear Wall Thickness 1. Calculate total lateral force per wall using tributary area method. 2. Let�s assume a tributary width of 6 meters for each wall. 3. F w a l l = T o t a l L o a d N u m b e r o f W a l l s = 80 k N 4 = 20 k N F_{wall}=\frac{Total Load}{Number of Walls}=\frac{80kN}{4}=20kN Fwall?=









.png)
